LETHE: A Tool for Uniform Interpolation and Related Reasoning Tasks
LETHE is a tool for uniform interpolation and related tasks for OWL ontologies using expressive description logics. The current version comes with functionality for computing uniform interpolants, logical differences and TBox abduction, and can be used as a Java library and as a standalone tool.
At the core of LETHE is the computation of so-called uniform interpolants. A uniform interpolant is a restricted version of an ontology that only uses a specified set of concept and role names, while preserving all logical entailments over this set. So far, the description logics ALC, ALCH and SHQ are supported, where forgetting role names is not supported for SHQ yet and interpolating ABoxes is only supported for ALC ontologies. If an input ontology contains axioms that are not expressible in the respective description logic, they will be removed before the algorithm is applied.
If the input ontology is cyclic, the uniform interpolant cannot always be represented finitely without fixpoint operators. Since fixpoint operators are not supported by OWL, the prototype might add additional concept names to the output ontology that simulate the behaviour of fixpoint operators. Another possibility is to approximate the uniform interpolant based on a given parameter.
This page provides the download of LETHE, and describes how to compute uniform interpolants per command line, graphical interface or using LETHE as a library. It further describes how to use the library for computing logical differences and performing TBox abduction.
More information and technical details of the underlying methods can be found in the following publications:
Koopmann, P., Schmidt, R.A.: LETHE: A Saturation-Based Tool for Non-Classical Reasoning. In: Proc. ORE'15. CEUR-WS.org (2015). Link
Koopmann, P., Schmidt, R.A.: Uniform Interpolation and Forgetting for ALC Ontologies with ABoxes. In: Proc. AAAI-15. AAAI Press (2015). Link Long Manuscript Version
Koopmann, P., Schmidt, R.A.: Count and Forget: Uniform Interpolation of SHQ-Ontologies. In: Proc. IJCAR'14. Springer (2014) Link Long Manuscript Version
Koopmann, P., Schmidt, R.A.: Forgetting Concept and Role Symbols in ALCH-Ontologies. In: Proc. LPAR'13. Springer (2013). Link Long Manuscript Version.
If you have any queries, suggestions or noticed any problems or bugs, please send me a message: patrick.koopmann@tu-dresden.de
Download
Version 0.6 (2020-02-28)
- many bugfixes and optimisations since last version
- supports OWL-API 5.1.7
- now supports SH knowledge bases
- optionally use universal roles in output
- timeout and cancel functionality allowing to compute partial forgetting results
| Stand-alone application: | lethe-standalone-0.6.tar.gz |
| Library: | lethe_2.12-0.6.jar |
| Dependencies (ivy-file): | ivy-0.6.xml |
| Dependencies (pom-file): | lethe_2.12-0.6.pom |
Version 0.026 (2015)
- supports OWL-API 3.5
- three forgetting methods implemented (corresponding to above papers): for ALCH TBoxes, SHQ TBoxes (without role forgetting), and ALC knowledge bases
| Stand-alone application: | lethe-standalone-0.026.tar.gz |
| Library: | lethe_2.11-0.026.jar |
The stand-alone version contains a stand-alone jar-file of the implementation and bash scripts to run LETHE from the command line. All dependencies of are included in the jar-file, so that only a compatible java interpreter is neccessary to execute it. The jar-file has been tested with Java 1.8.0, as implemented in the 64-Bit edition of the OpenJDK Runtime environment.
The second link is provided in case someone wants to use the implementation in its own project. It contains classes related to LETHE. The library has the following dependencies of additional libraries that have to be in the classpath:
- Scala Library 2.11.6
- Scala Swing 2.10.5
- OWL-API 3.5.2
- HermiT 1.3.6
- zero-log_2.11 0.3.6
- Fastring_2.11 0.2.4
Computing Uniform Interpolants using the Graphical User Interface
LETHE comes with a simple graphical tool for computing uniform interpolants of smaller ontologies. To start it, just run the provided bash script:./lethe-ui.sh
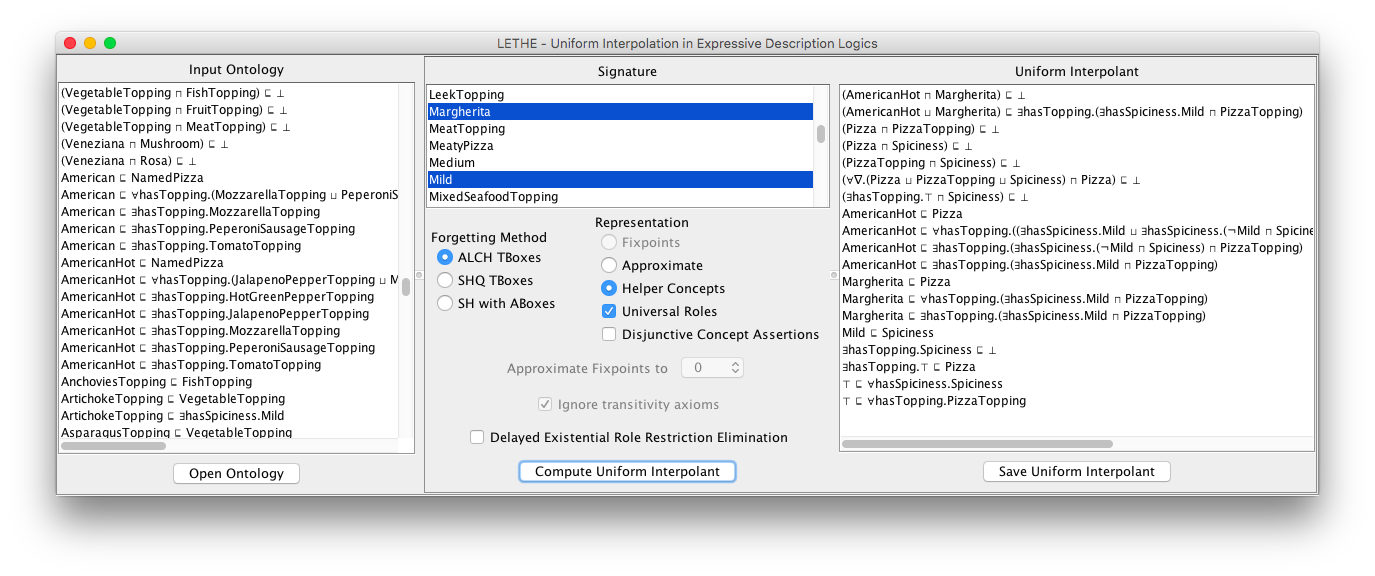
Using this tool, the user can open OWL files and compute uniform interpolants for a selected signature, as shown in the screenshot. The uniform interpolant is then displayed in DL syntax, and can be saved as OWL file for later use. LETHE implements three different methods for the description logics ALC, ALCH and SHQ, respectively denoted by ALCOntologyForgetter, ALCHTBoxForgetter and SHQTBoxForgetter. The ALCOntologyForgetter is capable of processing the ABox of an ontology as well, and the SHQTBoxForgetter only supports forgetting of concept symbols. The opened ontology is restricted to the supported description logic by removing axioms that cannot be represented in it.
If the input ontology is cyclic, it is possible that no finite OWL ontology can represent the uniform interpolant, unless if additional symbols are allowed. With the option "Helper Concepts", additional concept symbols may be used to represent these cycles. In the resulting ontology, all entailments of the uniform interpolant are preserved. With the option "Approximate", an approximation of the uniform interpolant is computed, that is completely in the desired signature and does not use helper concepts. The option "Disjunctive Concept Assertions" can speed up computations of uniform interpolants of ontologies with ABoxes, by using an extended logic to display the result.
Computing Uniform Interpolants from the Command Line
LETHE can also be used to compute uniform interpolants from the command lineThe ontology has to be provided either as an OWL file or as a URL pointing to the ontology. The full URIs of the names to be forgotten or to be included the signature of the uniform interpolant have to be provided in a text file, seperated by new lines. The tool can be used from the command line, using the provided bash script forget.sh, which is used as follows.
Get the list of provided options:
./forget.sh
Forget concept symbols in a given ontology:
./forget.sh --method METHOD --owlFile OWL_FILE --signature
SIGNATURE_FILE
./forget.sh --method METHOD --url ONTOLOGY_URL --signature SIGNATURE_FILE
Compute uniform interpolants for a given set of concept symbols
./forget.sh --interpolate --method METHOD --owlFile OWLFILE --signature SIGNATURE_FILE
./forget.sh --interpolate --method METHOD --url ONTOLOGY_URL --signature SIGNATURE_FILE
The parameter METHOD selects the method to be used, and has to be a number taken from the following list. If the parameter is omitted, ALCHTBoxForgetter is used as default value.
1 - ALCHTBoxForgetter
2 - SHQTBoxForgetter
3 - ALCOntologyForgetter
Computing Logical Difference from the Command Line
The logical difference of two ontologies O1 and O2 consists of the entailments of O2 in the common signature of O1 and O2, or a specified signature, which are not logically entailed by O1. It can be computed using the standalone version of LETHE in the following ways:
./logicalDifference.sh --owlFile1 FILE1 --owlFile2 FILE2
--approximationLevel LEVEL --method METHOD
./logicalDifference.sh --url1 URL1 --url2 URL2
--approximationLevel LEVEL --method METHOD
In addition, a parameter "--signature FILE" can be provided, where -- FILE points to a file containing the signature for which the logical difference is to be computed. METHOD is specified as described above, and LEVEL is an integer value specifying how much the logical difference is to be approximated in case the involved ontologies are cyclic.
The script computes a uniform interpolant of the second ontology and checks which of its axioms are entailed by the first ontology. The axioms which are not entailed represent the logical difference, and are stored in the OWL file "newEntailments.owl".
Usage of The Library: Uniform Interpolation
Depending whether the user wants to specify the signature of the uniform interpolant or a set of symbols to be forgotten, the LETHE offers two interfaces, IOWLInterpolator and IOWLForgetter. Both take as input an ontology object and a list of symbols, which are represented using the data types of the OWL API (see http://owlapi.sourceforge.net/ for further information). Depending on the expressivity of the input ontology, LETHE offers several implementations of these interfaces: the classes AlchTBoxInterpolator, ShqTBoxInterpolator and AlcOntologyInterpolator for uniform interpolation, and the classes AlchTBoxForgetter, ShqTBoxForgetter and AlcOntologyForgetter for forgetting. Axioms present in the ontology that are not supported by the method used will be removed by the implementation. Only AlcOntologyInterpolator and AlcOntologyForgetter support ABoxes, and ShqTBoxInterpolator and ShqTBoxForgetter do not support forgetting roles yet. Here is how the library is used in Java, exemplary for the case of a TBox in the description logic ALCH:
import uk.ac.man.cs.koopmanp.IOWLInterpolator
import uk.ac.man.cs.koopmanp.IOWLForgetter
import uk.ac.man.cs.koopmanp.AlchTBoxInterpolator
import uk.ac.man.cs.koopmanp.AlchTBoxForgetter
import org.semanticweb.owlapi.model.OWLEntity
import org.semanticweb.owlapi.model.OWLOntology
...
OWLOntology inputOntology;
Set<OWLEntity> symbols;
....
// computing the uniform interpolant over a given set of concept symbols:
IOWLInterpolator interpolator = new AlchTBoxInterpolator();
OWLOntology interpolant =
interpolator.uniformInterpolant(inputOntology, symbols);
// forgetting a set of concept symbols from a given ontology:
IOWLForgetter forgetter = new AlchTBoxForgetter();
OWLOntology forgettingResult = forgetter.forget(inputOntology, symbols);
Usage of the Library: Logical Difference
Logical Differences are computed using the class LogicalDifferenceComputer, which is instantiated using an IOWLInterpolator object. It is used as follows:
import uk.ac.man.cs.koopmanp.IOWLInterpolator
import uk.ac.man.cs.koopmanp.LogicalDifferenceComputer
import org.semanticweb.owlapi.model.OWLLogicalAxiom
import org.semanticweb.owlapi.model.OWLEntity
import org.semanticweb.owlapi.model.OWLOntology
...
OWLOntology ontology1;
OWLOntology ontology2;
Set<OWLEntity> signature;
int approximationLevel = 10;
IOWLInterpolator interpolator;
// Initialise values
...
LogicalDifferenceComputer ldc = new
LogicalDifferenceComputer(interpolator);
// Compute Logical Difference for common signature of the two ontologies:
Set<OWLLogicalAxiom> diff =
ldc.logicalDifference(ontology1, ontology2, approximationLevel)
// Compute Logical Difference for specified signature
Set<OWLLogicalAxiom> diff =
ldc.logicalDifference(ontology1, ontology2, signature, approximationLevel)
Usage of the Library: TBox Abduction
TBox abduction in LETHE is defined in the following way. We are given an ontology O of background knowledge, an observation T in form of a TBox axioms, and a signature S of "abducibles". The result of TBox abduction is then a set of axioms that is completely in the specified signature, and logically entails the observation if added to the ontology O.The kind of abduction that is implemented in LETHE is illustrated by the following example run:
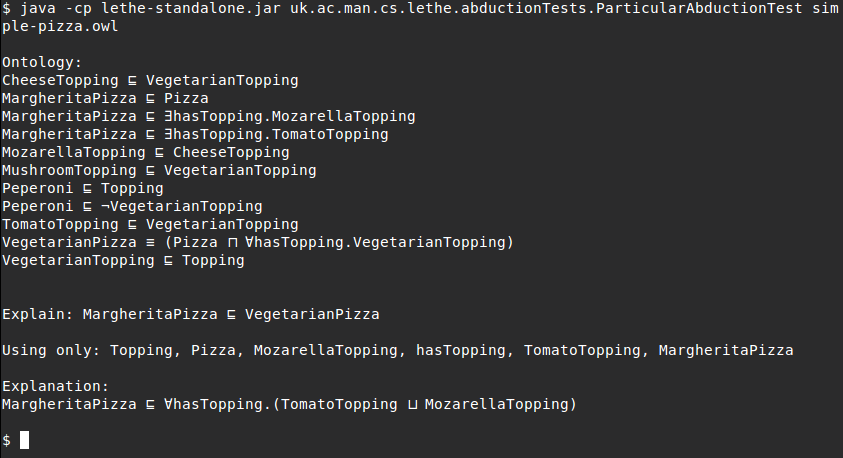
Roughly, abduction is implemented in LETHE by negating the observation, computing the uniform interpolant of the negated observation and the ontology of background knowledge, and then negating again the part of the uniform interpolant that corresponds to the (existentially quantified) negated observation.
TBox abduction is implemented in the class
OWLAbducer. Currently, LETHE only supports TBox abduction for
the description logic ALCH, and only for acyclic TBoxes. The
class OWLAbducer is used as follows:
import uk.ac.man.cs.koopmanp.AlchTBoxInterpolatorC
import uk.ac.man.cs.koopmanp.OWLAbducer
import uk.ac.man.cs.koopmanp.Explanation
import org.semanticweb.owlapi.model.OWLEntity
import org.semanticweb.owlapi.model.OWLOntology
...
OWLOntology ontology;
Set<OWLEntity> signature;
Set<OWLAxiom> observations;
...
AlchTBoxInterpolatorC interpolator = new
AlchTBoxInterpolatorC();
OWLAbducer abducer = new OWLAbducerSignatureBased(interpolator, ontology);
abducer.setAbducibles(signature);
Set<Explanation> explanation =
abducer.abduce(observations);
...
// Each Explanation object contains a set of TBox axioms which
is sufficient to be added to the ontology in order
// to entail the observation.
Explanation explanation = ...
Set<OWLAxiom> axioms = explanation.getAxioms();