In Theoretical Computer Science, the connection between finite automata and logics has been investigated intensively since the 1960s, starting with the seminal results by Büchi and Elgot showing the equivalence of Büchi automata and Monadic Second-Order Logic (MSO), and by McNaughton and Papert showing the equivalence of star-free languages and First-Order Logic (FOL). These results were first shown for words (as input for the automata or interpretation structures for the logics), but then extended by Rabin and others to trees. From the logician's point of view, this connection can, e.g., be used to compare the expressiveness of different logics and to obtain decision procedures for the logic. Decidability of MSO follows from its connection to Büchi automata, and this decidability result can in turn be used to show decidability of many application-relevant sublogics (such as the modal mu-calculus and certain temporal and description logics). In order to obtain decision procedures with worst-case optimal complexity for these sublogics, more specialized approaches need to be employed, which may, however, again be based on the use of appropriate automata models. For example, any formula of Linear Temporal Logic (LTL) can be translated into a corresponding Büchi automaton that accept exactly the models of the formula, and this connection can be used to show that the satisfiability problem for LTL can be solved using only polynomial space. Interestingly, LTL has the same expressive power as FOL, i.e., LTL formulae also define exactly the star-free languages, but the FOL representation of a given star-free language may be exponentially more succinct than the LTL representation. Due to the plethora of available results on the connection between logics and automata, we have mentioned only some of the classical results, and refer to pertinent overview articles such as [1,2] for more information.
The logics and automata models mentioned above support modelling of qualitative properties only. However, in many Computer Science applications, quantitative properties need to be represented as well. To overcome this deficit on the logical side, quantitative logics were developed, where we subsume under this notion both logics with richer sets of truth values (such as multi-valued logics, fuzzy logics, and probabilistic and possibilistic logics) and logics that can model quantitative aspects of the world (such as space, time, similarity, and resource consumption). For some of these logics, specialized quantitative automata models were introduced. On the automata side, classical automata models were directly extended to quantitative variants, called weighted automata (on finite or infinite words or trees). Research on the connection between weighted automata and quantitative logics has started only recently.
Summing up, one can say that that the connection between logics and automata is also important on the quantitative side, but has not been investigated in such a comprehensive way as in the classical case. The unique feature of this research training group is the theoretically well-founded and comprehensive investigation of quantitative logics and automata, their connections, and their usefulness in not only one, but several substantially different application areas. Previous works and research projects were either focused on investigating one of the two models (quantitative automata or quantitative logics), or considered their connection in the context of a specific application.
Following the expertise of the supervising professors and associated members, the research carried out in the research training group will draw its motivations from the application areas verification, knowledge representation, and constraint satisfaction. For example, in the area of verification, reactive systems are modelled using finite automata and (desired or forbidden) properties are defined using an appropriate temporal logic (such as LTL or CTL). Model checking then tests fully automatically whether the system has the property. One way of realizing this is to translate the formula (or its negation) into an automaton that accepts its models. In knowledge representation, one often employs decidable logics that provide a good compromise between expressiveness and the complexity of reasoning. Automata-based reasoning approaches often yield worst-case optimal decision procedures (e.g., for certain modal, temporal, and description logics), whereas this is harder to achieve for other reasoning approaches (such as tableau procedures). Constraint Satisfaction Problems (CSPs) are computational problems where the input consists of a set of variables together with constraints restricting their values (such as equations and inequations). The question is then whether there is a valuation of the variables satisfying all constraints. The computational complexity of CSPs has been extensively studied, first mainly for CSP over finite sets of values, but now also more and more for infinite-valued CSPs. When investigating the complexity of CSPs, algebraic and logical approaches have turned out to be very useful. There is also a close connection between CSPs and certain decision problems in knowledge representation. In all these application areas, the representation and processing of quantitative aspects is important.
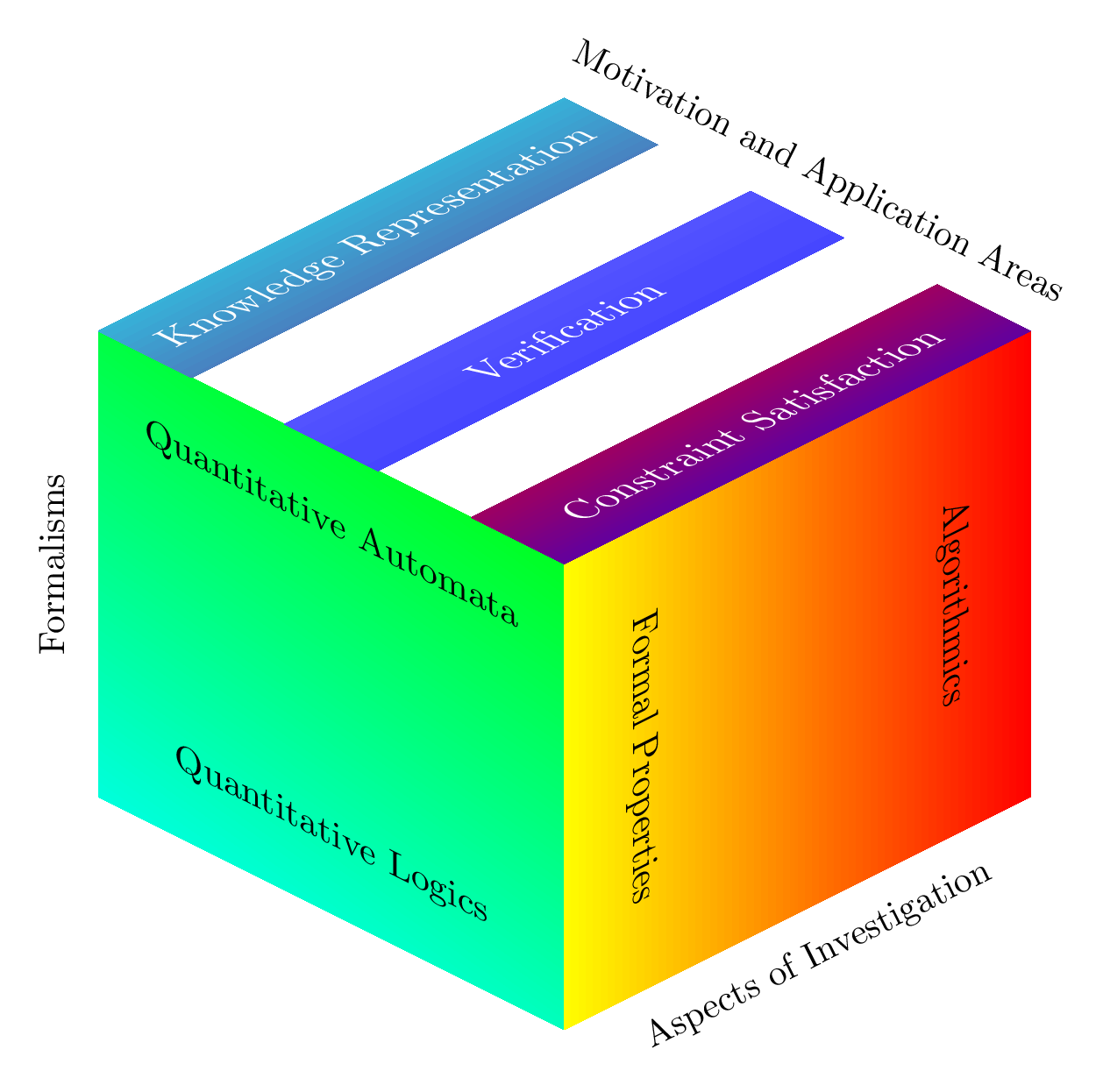
To structure the research programme of QuantLA, we consider three different dimensions: the formalism dimension, the motivation and application dimension, and the research facet dimension. On the formalism dimension, we distinguish whether the research objects are quantitative automata or quantitative logics, and on a more fain-grained level which kind of quantitative information (probabilities, fuzzy values, weights in a semiring, etc.) are considered. Of course, these facets are not disjoint; in particular, investigating the connection between quantitative automata and quantitative logics will be an important topic. On the motivation and application dimension, we consider the three application areas mentioned above. The research topics will usually be motivated by one of these areas, though some purely theoretically motivated topics are also possible. Regarding the research facets, we distinguish between the investigation of formal properties, such as expressiveness of a logic or automata model, model- or proof-theoretic properties of a logic, and closure properties of an automata model, and of algorithmic properties, such as complexity of reasoning in a logic and decision problems for automata (e.g., emptiness and inclusion problem). In the quantitative case, not only decision problems, but also computation problems are important. For example, if a system is modelled using a weighted automaton, one may be interested in computing the maximal or minimal costs for reaching a certain goal state. The two facets are not independent, but may influence each other. For instance, model-theoretic properties of a logic (finite model property, tree model property) may be relevant for the design of decision procedures.
- W. Thomas. Languages, automata, and logic. In Handbook of Formal Languages, pages 389 –455. Springer-Verlag, 1996.
- E. Grädel, W. Thomas, and T. Wilke, editors. Automata, Logics, and Infinite Games: A Guide to Current Research, volume 2500 of Lecture Notes in Computer Science. Springer-Verlag, 2002.